緑進塾　授業の生中継


	サイトメニュー
	□トップ　□募集要綱　□授業生中継　□お問い合わせ □アクセス　□個人情報の取り扱い　□リンク

中２・３では、このようなことにチャレンジしています！
じっくり考えて糸口がみつかる面白さをぜひいっしょに体験しましょう！

例問１　：

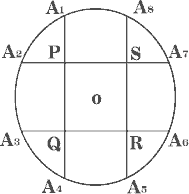
図のように、半径aの円Oの周を８等分する点を順に、A１、A２、……、A８とし、弦A1A4と弦A２A7、A3A6との交点をそれぞれP、Qとし、弦A５A8とA3A6、A2A7との交点をそれぞれR、Sとする。
このとき、正方形PQRSの面積を求めよ。また線分A1P、A2Pと弧A1A2とで囲まれる図形の面積を求めよ。

(昭和55年　東京大学文系2次試験・数学）

＜解説＞

あの東大の数学の問題！ですが、三角関数を知らなくとも、中学で学ぶ三平方の定理までの知識を駆使すれば、なんと見事に解決してしまいます！
授業ではそのエッセンスを提示しています。

例問２　：　

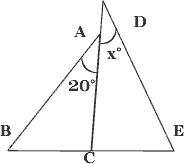
図において、３点Ｂ、Ｃ、Ｅは一直線上にあり、ＡＢ＝ＤＥ、ＢＣ＝ＥＣ、∠ＢＡＣ＝２０°である。
このとき、∠ＣＤＥは何度か。

＜解説＞

実にシンプルな問題ですが、当塾講師が現役時代に出会った中で、いまだに忘れられない興味深い問題です。
あっと驚く補助線が飛び出し、中２までの知識で解決できます！
この問題に限らず、初等幾何の名問を数多く、時間をかけて解くことで、集中力・諦めない心が訓練されます。

□トップ　□募集要綱　□授業生中継　□お問い合わせ　□アクセス　□個人情報の取り扱い　□リンク